chapter 1
 section 1.1
section 1.1
STATISTICAL MECHANICS AND COMPUTER SIMULATION
The state of a liter of water can be described using only a few
macroscopic equilibrium properties. This is remarkable, considering
that the fluid consists of some 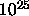 mutually interacting atoms.
The secret lies in the word macroscopic. All atomic processes
and fluctuations take place extremely fast on a very small distance
scale and will be averaged out while we perform our measurement. Only
those particular combinations of atomic coordinates that are
essentially time independent can be macroscopic observable. To compute
the equilibrium properties of a bulk substance, there is little need
to know the exact trajectory of every atom in the system. Rather, we
like to calculate the average properties starting from a proper
atomistic model. Thermodynamics relates macroscopic equilibrium
properties with each other and statistical mechanics provides the link
between these quantities and the atomistic description on a
microscopic level [1,2].
mutually interacting atoms.
The secret lies in the word macroscopic. All atomic processes
and fluctuations take place extremely fast on a very small distance
scale and will be averaged out while we perform our measurement. Only
those particular combinations of atomic coordinates that are
essentially time independent can be macroscopic observable. To compute
the equilibrium properties of a bulk substance, there is little need
to know the exact trajectory of every atom in the system. Rather, we
like to calculate the average properties starting from a proper
atomistic model. Thermodynamics relates macroscopic equilibrium
properties with each other and statistical mechanics provides the link
between these quantities and the atomistic description on a
microscopic level [1,2].
The fundamental quantity in equilibrium statistical mechanics is
the partition function, the sum of the Boltzmann factors over all
possible states s of a canonical system of N atoms in a volume V
at a temperature T

Here 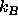 is Boltzmann 's constant and
is Boltzmann 's constant and 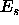 is the total energy of
the system in state s.
The Boltzmann factors
is the total energy of
the system in state s.
The Boltzmann factors 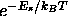 are proportional to the
probability of finding the system in state s. One therefore can also
calculate the average of any dynamical property A as
are proportional to the
probability of finding the system in state s. One therefore can also
calculate the average of any dynamical property A as

The ergodic theorem states that this ensemble average 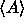 is equal to the time
average of A that would be obtained by following the natural dynamics
of the system for a sufficiently long time [2]. The canonical partition
function Z is connected to the thermodynamic Helmholtz free energy F by
is equal to the time
average of A that would be obtained by following the natural dynamics
of the system for a sufficiently long time [2]. The canonical partition
function Z is connected to the thermodynamic Helmholtz free energy F by

The average value of most equilibrium properties is related in one way or another to (derivatives of) the Helmholtz free energy F, and can therefore be expressed in terms of the partition function Z.
For instance, the energy E can be
calculated as follows,

In view of the central role played by the partition function, the aim
of many theoretical studies in equilibrium statistical mechanics is
to find (approximate) expressions for the partition function, for
specific model systems.
An alternative route to extract the macroscopic
information from a microscopic model, is to perform computer
simulations [3]. There are two basic styles of computer
simulations:
Monte Carlo (MC) and molecular dynamics (MD). In an MD simulation one
solves Newton's equation of motion numerically for a system
containing several hundreds up to several millions of molecules,
in discrete time steps. The desired macroscopic observables are computed
simply by
time averaging. Hence, the MD simulation follows the natural
time evolution of the system, which includes dynamical information.
With the use of periodic boundaries, a small number of atoms (usually
100-10000) is usually already enough to
approximate the behavior of an infinite system.
The Monte Carlo method
can be considered a numerical implementation of Gibbs' concept of
averaging over an ensemble of equilibrium states:
in MC simulations, macroscopic observables are obtained by directly
computing properly weighted averages over the accessible states of a
many-particle system (cf. eqn.
1.2). Because
the order in which this averaging is carried out has no physical
meaning, the MC method contains no
dynamical information.
In practice, the averaging over the most probable states of this
system is achieved by using a
random sampling procedure. Starting from a configuration, one or more
particles are
moved randomly. Each move is accepted or rejected with a certain
probability, such that the probability of finding the system in a state
s is proportional to the Boltzmann factor 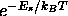 (in
practice, only the potential energy
(in
practice, only the potential energy 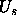 needs to be considered in
this sampling).
needs to be considered in
this sampling).
As computer simulations of classical many-body systems are, in
principle, exact (i.e. can be carried out to any desired accuracy),
they can be used to test the assumptions made in approximate theories
of many-body systems.
Simulations are also of great practical use in predicting the
macroscopic properties of new
materials or novel substances,
before embarking on the expensive task of actually making these materials.
Moreover, computer simulations can be used to asses the behavior of
materials under
conditions that are not easily achieved in experiments. Finally,
computer simulations sometimes allow us to predict qualitatively
new behavior, or new phases of known substances, and thereby act as a guide
to both theoretical and experimental work.
chapter 1
 section 1.1
section 1.1
Peter Bolhuis
Tue Sep 24 20:44:02 MDT 1996
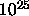 mutually interacting atoms.
The secret lies in the word macroscopic. All atomic processes
and fluctuations take place extremely fast on a very small distance
scale and will be averaged out while we perform our measurement. Only
those particular combinations of atomic coordinates that are
essentially time independent can be macroscopic observable. To compute
the equilibrium properties of a bulk substance, there is little need
to know the exact trajectory of every atom in the system. Rather, we
like to calculate the average properties starting from a proper
atomistic model. Thermodynamics relates macroscopic equilibrium
properties with each other and statistical mechanics provides the link
between these quantities and the atomistic description on a
microscopic level [1,2].
mutually interacting atoms.
The secret lies in the word macroscopic. All atomic processes
and fluctuations take place extremely fast on a very small distance
scale and will be averaged out while we perform our measurement. Only
those particular combinations of atomic coordinates that are
essentially time independent can be macroscopic observable. To compute
the equilibrium properties of a bulk substance, there is little need
to know the exact trajectory of every atom in the system. Rather, we
like to calculate the average properties starting from a proper
atomistic model. Thermodynamics relates macroscopic equilibrium
properties with each other and statistical mechanics provides the link
between these quantities and the atomistic description on a
microscopic level [1,2].

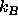 is Boltzmann 's constant and
is Boltzmann 's constant and 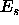 is the total energy of
the system in state s.
The Boltzmann factors
is the total energy of
the system in state s.
The Boltzmann factors 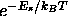 are proportional to the
probability of finding the system in state s. One therefore can also
calculate the average of any dynamical property A as
are proportional to the
probability of finding the system in state s. One therefore can also
calculate the average of any dynamical property A as

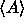 is equal to the time
average of A that would be obtained by following the natural dynamics
of the system for a sufficiently long time [
is equal to the time
average of A that would be obtained by following the natural dynamics
of the system for a sufficiently long time [

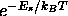 (in
practice, only the potential energy
(in
practice, only the potential energy 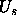 needs to be considered in
this sampling).
needs to be considered in
this sampling).