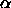 , we reduce all diameters by a factor
, we reduce all diameters by a factor
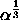 . In addition to more directly coupling the
diameter and volume changes, this move is appealing because it
requires no overlap test. The acceptance probability for this combined
move is
. In addition to more directly coupling the
diameter and volume changes, this move is appealing because it
requires no overlap test. The acceptance probability for this combined
move is
Application of a standard Monte Carlo algorithm yielded very poor
statistics. This outcome is probably caused by the inability of the
volume to adjust quickly to particle diameter changes, and vice
versa. A remedy might be to introduce a combined volume- and
diameter-change Monte Carlo step: while reducing the volume by a
factor 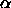 , we reduce all diameters by a factor
, we reduce all diameters by a factor
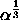 . In addition to more directly coupling the
diameter and volume changes, this move is appealing because it
requires no overlap test. The acceptance probability for this combined
move is
. In addition to more directly coupling the
diameter and volume changes, this move is appealing because it
requires no overlap test. The acceptance probability for this combined
move is
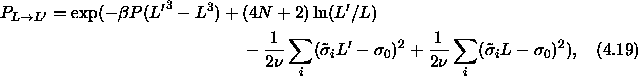
where L is the length of the cubic box with volume 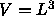 and
and
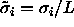 are the scaled diameters. Although
this method will produce better results, we can improve the scheme
even more by scaling both the diameters and the coordinates, thereby
permitting (near-) analytic evaluation of the volume
integral. Consider the configurational part of the isobaric semigrand
partition function
are the scaled diameters. Although
this method will produce better results, we can improve the scheme
even more by scaling both the diameters and the coordinates, thereby
permitting (near-) analytic evaluation of the volume
integral. Consider the configurational part of the isobaric semigrand
partition function
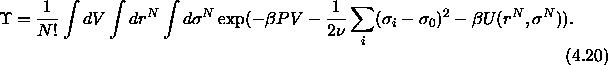
If we now introduce scaled coordinates and diameters 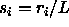 and
and
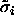 as above the partition function can be written as
as above the partition function can be written as
The outermost two integrals do not contain any volume
dependence. Moreover, the 'weighting function' 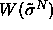 defined here can be evaluated entirely at every Monte Carlo move. In
this way, there is no need for volume sampling at all. Instead, at
every move we obtain the average volume by evaluating
defined here can be evaluated entirely at every Monte Carlo move. In
this way, there is no need for volume sampling at all. Instead, at
every move we obtain the average volume by evaluating
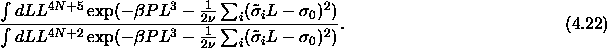
In this scaling method there are only two kinds of Monte Carlo moves: the regular particle displacements and the diameter changes. Both changes are made in the scaled variables. The acceptance probabilities are

where 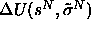 is the change in potential
energy associated with the move. If a particle's diameter is changed
the integral
is the change in potential
energy associated with the move. If a particle's diameter is changed
the integral 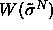 must be reevaluated. Because the
exponential in the integral is a cubic polynomial this cannot be done
analytically. However, if we write the integral as
must be reevaluated. Because the
exponential in the integral is a cubic polynomial this cannot be done
analytically. However, if we write the integral as

we can approximate it accurately by applying the method of steepest
descent. Replacing the function 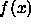 by a second-order Taylor
expansion around the maximum of
by a second-order Taylor
expansion around the maximum of 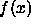 yields
yields
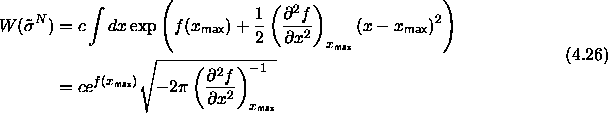
This approximation is possible because the function 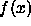 is large
(being proportional to N) and it drops quickly away from the maximum.
is large
(being proportional to N) and it drops quickly away from the maximum.
| Figure: |
Solid-fluid coexistence pressure as a function of variance of the imposed activity distribution. In the inset
the pressure is reduced to 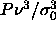 to show the limiting behavior. to show the limiting behavior.
|
| Figure: | Coexistence pressure of the solid (left curve) and the fluid (right curve) as a function of the width of the composition distribution, the polydispersity s. |