chapter 3
 section 3.7
section 3.7
Simple solids with a short ranged attractive pair potential can exhibit
phase separation in a expanded
solid and a more dense solid. This isostructural first-order
solid-solid transition is reminiscent of the liquid-vapor transition.
The transition takes place between two phases of the same structure,
the coexistence curve ends in a critical point and the location of
the coexistence curves depends strongly on the interaction range.
The simulations on the square-well model show that the solid-solid
transition takes place both in two and three dimensions for potential
well-widths 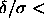 0.07.
The analogy with liquid-vapor phase separation suggests that the
solid-solid critical point should be of the 2D and 3D Ising
universality class, although this still remains to be established.
The critical density depends on the well-width
0.07.
The analogy with liquid-vapor phase separation suggests that the
solid-solid critical point should be of the 2D and 3D Ising
universality class, although this still remains to be established.
The critical density depends on the well-width  and is well
predicted by the uncorrelated cell-model. In contrast, the critical
temperature hardly changes with
and is well
predicted by the uncorrelated cell-model. In contrast, the critical
temperature hardly changes with  .
The critical temperature is finite for
.
The critical temperature is finite for 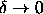 . This
has been confirmed by direct simulations in this limit.
Comparison of the adhesive sphere model theories with the simulations
in the limit
. This
has been confirmed by direct simulations in this limit.
Comparison of the adhesive sphere model theories with the simulations
in the limit 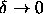 shows that the solid-solid
transition already occurs for
shows that the solid-solid
transition already occurs for 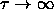 , where
, where  plays the role of temperature in the adhesive sphere model. This
implies that at finite
plays the role of temperature in the adhesive sphere model. This
implies that at finite  the only stable phases are the
close-packed solid and a the infinite dilute gas. All other phases
are, at best, meta-stable. This pathological behavior is thought to
be a consequence of the monodispersity of the system. We expect that
introducing a slight size polydispersity will cause the solid-solid
transition to occur at finite
the only stable phases are the
close-packed solid and a the infinite dilute gas. All other phases
are, at best, meta-stable. This pathological behavior is thought to
be a consequence of the monodispersity of the system. We expect that
introducing a slight size polydispersity will cause the solid-solid
transition to occur at finite  .
.
The results for the solid-solid transition in Yukawa systems are
comparable to those for the square-well model. The solid-solid
transition occurs for 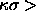 25, i.e. a potential well
width narrower than 0.04
25, i.e. a potential well
width narrower than 0.04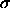 . The major difference with the
square-well results is that the critical temperature depends more
strongly on
. The major difference with the
square-well results is that the critical temperature depends more
strongly on  .
.
An isostructural solid-solid transition, induced by the mechanism
described above, will also occur in systems
with repulsive ``square shoulder'' potentials.
The critical temperatures are almost equal to that of the square well
system, but the critical densities are significantly higher.
Led by the theoretical work of Stell and Hemmer [52] and
Kincaid, Stell and Goldmark [72] we have extrapolated the solid-solid
binodals to T=0, where effectively two close packed solids are in coexistence.
An obvious question is whether the isostructural solid-solid phase
transition due to short-ranged attraction, that we report here, can
occur in real systems.
We believe that such a transition can be observed in uncharged colloids
with a short-ranged attraction. Such systems can be made, as we
discussed in the previous chapters,
by adding
non-adsorbing polymer to a suspension of hard-sphere colloids (for a review,
see e.g. ref. [8]). The polymers induce an effective attractive force
between the colloidal spheres. The range of this attraction is directly related
to the radius of gyration of the polymer.
Hence, a colloidal crystal to which a polymer with a radius
of gyration less than 7% of the radius of the colloidal spheres has
been added, should exhibit the solid-solid phase behavior of the
models discussed in this chapter.
However, introducing size polydispersity in the colloidal system will decrease the
stability of the solid-solid transition.
Our simulations show that for a colloidal dispersion with a polydispersity
of more than 1% the solid-solid transition has become metastable with
respect to the fluid-solid transition.
chapter 3
 section 3.7
section 3.7
Peter Bolhuis
Tue Sep 24 20:44:02 MDT 1996
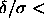 0.07.
The analogy with liquid-vapor phase separation suggests that the
solid-solid critical point should be of the 2D and 3D Ising
universality class, although this still remains to be established.
The critical density depends on the well-width
0.07.
The analogy with liquid-vapor phase separation suggests that the
solid-solid critical point should be of the 2D and 3D Ising
universality class, although this still remains to be established.
The critical density depends on the well-width  and is well
predicted by the uncorrelated cell-model. In contrast, the critical
temperature hardly changes with
and is well
predicted by the uncorrelated cell-model. In contrast, the critical
temperature hardly changes with  .
The critical temperature is finite for
.
The critical temperature is finite for 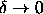 . This
has been confirmed by direct simulations in this limit.
Comparison of the adhesive sphere model theories with the simulations
in the limit
. This
has been confirmed by direct simulations in this limit.
Comparison of the adhesive sphere model theories with the simulations
in the limit 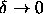 shows that the solid-solid
transition already occurs for
shows that the solid-solid
transition already occurs for 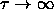 , where
, where  plays the role of temperature in the adhesive sphere model. This
implies that at finite
plays the role of temperature in the adhesive sphere model. This
implies that at finite  the only stable phases are the
close-packed solid and a the infinite dilute gas. All other phases
are, at best, meta-stable. This pathological behavior is thought to
be a consequence of the monodispersity of the system. We expect that
introducing a slight size polydispersity will cause the solid-solid
transition to occur at finite
the only stable phases are the
close-packed solid and a the infinite dilute gas. All other phases
are, at best, meta-stable. This pathological behavior is thought to
be a consequence of the monodispersity of the system. We expect that
introducing a slight size polydispersity will cause the solid-solid
transition to occur at finite  .
. 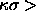 25, i.e. a potential well
width narrower than 0.04
25, i.e. a potential well
width narrower than 0.04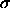 . The major difference with the
square-well results is that the critical temperature depends more
strongly on
. The major difference with the
square-well results is that the critical temperature depends more
strongly on  .
.